變分自動編碼器 Variational Autoencoder：理論篇

簡介

變分自動編碼器(Variational Autoencoder, VAE)的概念是由 Diederik P. Kingma 與 Max Welling 在論文《Auto-Encoding Variational Bayes》所提出，其利用貝式定理進行 變分推斷 ，之中還運用了 重參數化 (reparameterization)來預估ELBO，使其可用常見的優化器來最佳化。^[1]其結構和自動編碼器(Autoencoder, AE)類似，一樣以編碼器和解碼器組成，並且在學習潛在向量 z 的同時，還要做到重構(reconstruct)資料。不同的地方是：相較於AE，VAE會 嘗試從一個可編碼的連續潛在空間去對應輸入的分配建模 。且 VAE 把解碼器當成生成模型來使用，這使其具備 生成性 (generative)。^[2]

VAE 的目標

生成模型的目標是運用神經網路來近似輸入資料(圖像等)的真實分配：

$$\begin{equation}x\sim P_{\theta}(x)\end{equation}$$

其中$\theta$是在訓練過程中所決定的參數。(如：找到可繪製各種臉部的分配)

要做到一定程度的推論，需要找到$P_{\theta}(x,z)$，也就是輸入$x$與潛在變數$z$之間的聯合分配。其中潛在變數$z$是由輸入的特徵編碼而來(如：臉部的五官、表情等)。而$P_{\theta}(x,z)$可由邊際分配求出，如下式：

$$\begin{equation} P_{\theta}(x)=\int_{}^{}P_{\theta}(x,z)dz \end{equation}$$

簡單來說，我們希望可以建構一個可描述輸入資料的分配(如：眼睛大、鼻子挺、嘴巴小的男性臉部)。而其中的一大難處在於，式 2 是 難解的 (intractable)，因為它不具備任何分析形式或有效的估計量。原因如下：

1. 將式 2 以貝式定理的乘法法則改寫成如下式時：

   $$\begin{equation} P_{\theta}(x)=\int_{}^{}P_{\theta}(x|z)P(z)dz \end{equation}$$

   其中$P_{\theta}(x|z)$是$z$的事前機率，也就是沒有對任何觀察值加上條件。我們可以有兩種假設：

   • 假設$z$是離散，且$P_{\theta}(x)$是高斯分配，則$P_{\theta}(x)$是一個高斯混合。
   • 假設$z$為連續，則$P_{\theta}(x|z)$是無限高斯混合。

   如果沒有一個合適的損失函數去近似$P_{\theta}(x|z)$，則會直接忽略$z$，並得到$P_{\theta}(x|z)=P_{\theta}(x)$。這樣一來，我們無從得知$P_{\theta}(x)$的估計值。

2. 將式 2 改寫成如下式時：

   $$\begin{equation} P_{\theta}(x)=\int_{}^{}P_{\theta}(z|x)P(x)dz \end{equation}$$

   此式中的$P_{\theta}(z|x)$同樣不可解。

為了可以估計$P_{\theta}(z|x)$，我們可以使用變分推斷(variational inference)去找到一個可解的分配。也就是說， VAE 的目標是近似$P_{\theta}(z|x)$ 。

變分推斷(Variational Inference)

VAE 採用了變分推斷模型作為編碼器來近似$P_{\theta}(z|x)$，如下式：

$$\begin{equation}Q_{\phi}(z|x)\approx P_{\theta}(z|x)\end{equation}$$

$Q_{\phi}(z|x)$是$P_{\theta}(z|x)$的估計值，透過最佳化參數$\phi$，$Q_{\phi}(z|x)$就可利用深度神經網路來求近似使其可解。我們可以使用 多變量高斯 來挑選$Q_{\phi}(z|x)$，如下式：

$$\begin{equation}Q_{\phi}(z|x)\approx \mathcal{N}(z;\mu(x),diag(\sigma(x)))\end{equation}$$

其中的平均數$\mu(x)$與標準差$\sigma(x)$可由編碼器使用輸入的資料來計算，且其中的對角矩陣表示$z$的元素彼此獨立。

損失函數(Loss Fuction)推導

我們可以使用 KL 散度 (Kullback-Leibler divergence)來計算$Q_{\phi}(z|x)$$P_{\theta}(z|x)$之間的誤差(可視作某種距離)。(KL 散度簡介見補充1.)如下式：

$$\begin{equation}D_{KL}(Q_{\phi}(z|x)||P_{\theta}(z|x))=\mathbb{E}_{z\sim Q}[logQ_{\phi}(z|x)-logP_{\theta}(z|x)]\end{equation}$$

使用貝式定理

$$\begin{equation}P_{\theta}(z|x)=\frac{P_{\theta}(x|z)P_{\theta}(z)}{P_{\theta}(x)}\end{equation}$$

來展開式 7，如下式：

$$\begin{equation}\begin{split}D_{KL}(Q_{\phi}(z|x)||P_{\theta}(z|x))& =\\ \mathbb{E}_{z\sim Q}[logQ_{\phi}(z|x)&-logP_{\theta}(x|z)-logP_{\theta}(x)]+logP_{\theta}(x)\end{split}\end{equation}$$

由於$z \sim Q$並不相依，上式中的$logP_{\theta}(x)$可視作是一個微分常量，故可重新整理後可得如下式：

$$\begin{equation}\begin{split} logP_{\theta}(x)-D_{KL}(Q_{\phi}(z|x)||P_{\theta}(z|x))&=\\ \mathbb{E}_{z\sim Q}[logP_{\theta}(z|x)]-D_{KL}&(Q_{\phi}(z|x)||P_{\theta}(x)) \end{split}\end{equation}$$

式 10 解釋：

• 左側：表示要最大化的$P_{\theta}(x)$減去近似分佈$Q_{\phi}(z|x)$與真實分佈$P_{\theta}(z|x)$的 KL 散度(誤差)，此處稱作變分下界(variational lower bound)或證據下界(evidence lower bound, ELBO)。由於 KL 散度永遠為正(距離的概念)，ELBO 就是$logP_{\theta}(x)$的下界。簡單來說，在最佳化$\phi$與$\theta$來最大化 ELBO 時，需最大化$P_{\theta}(x)$及最小化$D_{KL}$，來使 VAE 重構原資料的表現越來越好，如下式：

  $$\begin{equation}max P_{\theta}(x), minD_{KL}\end{equation}$$

• 右側：
  • 第一項$\mathbb{E}_{z\sim Q}[logP_{\theta}(z|x)]$： 類似於解碼器，將其最大化代表將重構損失$\mathcal{L}_{R}$最小化。《Auto-Encoding Variational Bayes》中給出兩種可能性：
    • 假設資料為 高斯分配 ，則損失函數$\mathcal{L}_{R}$為 均方誤差 (Mean-Square Error, MSE)。
    • 假設資料為白努利分配，則損失函數$\mathcal{L}_{R}$為二元交叉熵(binary cross entropy)。
  • 第二項$-D_{KL}(Q_{\phi}(z|x)||P_{\theta}(x))$：
    • 已知$Q_{\phi}(z|x)$為高斯分佈(式 6)，且$P_{\theta}(z)=P(z)=\mathcal{N}(0,I)$，其中平均數為 0，標準差為 1.0，則此項可簡化為：

      $$\begin{equation} -D_{KL}(Q_{\phi}(z|x)||P_{\theta}(x))=\frac{1}{2}\sum_{j=1}^{J}(1+log(\sigma_{j})^{2}-(\mu_{j})^{2}-(\sigma_{j})^{2}) \end{equation}$$

      其中$J$為$z$的維度；$\mu_{j}$與$\sigma_{j}$皆為推論計算中$x$的的函數，最大化$-D_{KL}$會使$\mu_{j}\to0$、$\sigma_{j}\to1$。由上式可得$\mathcal{L}_{KL}=D_{KL}$。

總結以上，可得 VAE 的損失函數$\mathcal{L}_{VAE}$為：

$$\begin{equation}\mathcal{L}_{VAE}=\mathcal{L}_{R}+\mathcal{L}_{KL}\end{equation}$$

重參數化(Reparameterization)

VAE 中為解決後向傳播時梯度無法經過隨機 sampling 的問題，將 sampling 過程重參數化，並視其為輸入的一部份，修改過程如下所示：

$$\begin{equation}[Sample=\mu+\sigma] \Rightarrow [Sample=\mu+\boxed{\in}\sigma]\end{equation}$$

其中$\in$為重參數取樣，並整併至標準差$\sigma$後，再與平均數$\mu$相加。

這樣一來，VAE 將可使用常用的 Optimizer(如：Adam)來最佳化。

VAE 架構總結

如圖1所示，左方為編碼器，其輸出不再直接輸出$z$，而是輸入資料$x$的平均數$\mu_{x}$與標準差$\sigma_{x}$。並同時從輸入資料$x$採樣得到$\in$後($\in$為高斯分佈)，進行如下式之運算，計算出潛在空間$z$：

$$\begin{equation}z=\mu_{x}+\sigma_{x}\circ \in\end{equation}$$

而圖1右方為解碼器，其在潛在空間$z$採樣並還原資料(如：圖像等)。

圖1 VAE架構圖

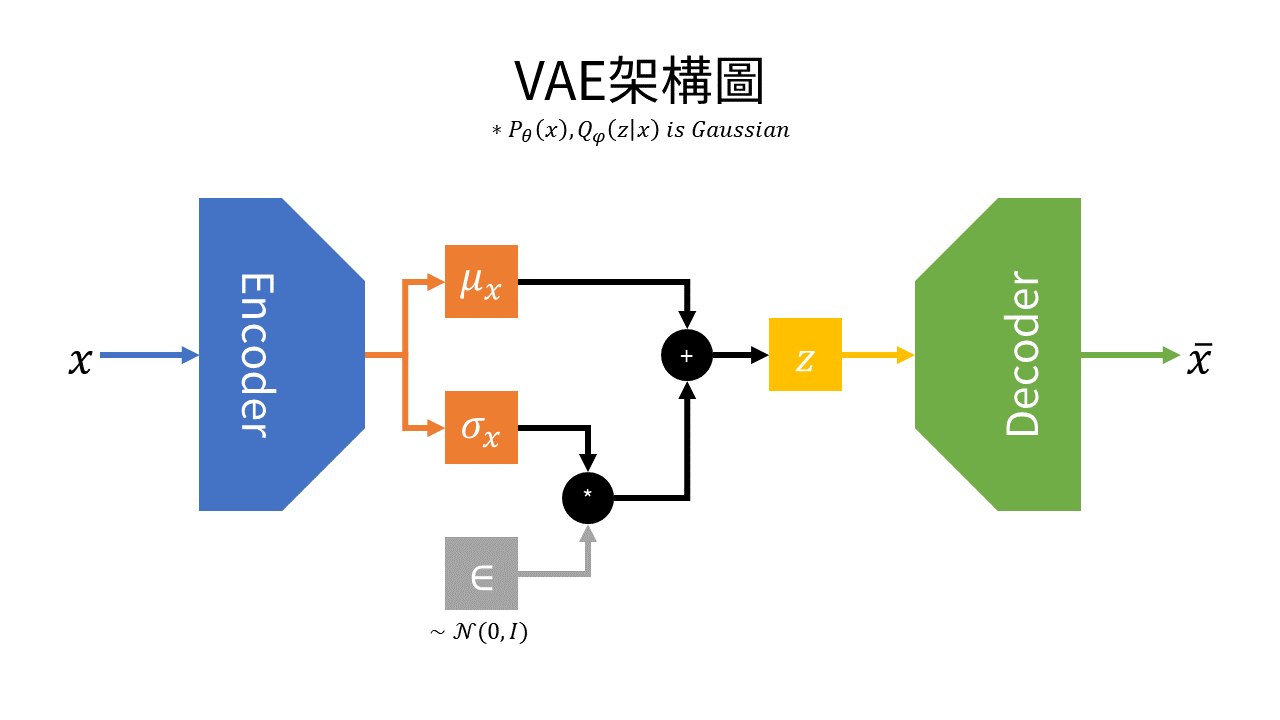
一般假設輸入資料分佈$P_{\theta}(x)$與近似分佈$Q_{\phi}(x)$皆為高斯分佈，則損失函數$\mathcal{L}_{VAE}$為：

$$\begin{equation} \begin{split} \mathcal{L}_{VAE}&=MSE+D_{KL}(P_{\theta}(x)||Q_{\phi}(x))\\&\simeq\frac{1}{L} \sum_{l=1}^{L}logP_{\theta}(x|z)+\frac{1}{2}\sum_{j=1}^{J}(1+log(\sigma_{x}^2)-\mu_{x}^2-\sigma_{x}^2) \end{split} \end{equation}$$

補充

1. KL 散度(Kullback-Leibler divergence, KLD)簡介

KL 散度是兩機率分佈$P$與$Q$之間的差距，其中$P$為真實分佈，$Q$為$P$的近似分佈。^[3]

• KL 散度為 非負值 ，如下式：

  $$\begin{equation} D_{KL}(P||Q)\ge 0 \end{equation}$$

• 雖然可將 KL 散度看作某種距離，但須注意其 不具對稱性 ，如下式：

  $$\begin{equation} D_{KL}(P||Q)\neq D_{KL}(Q||P) \end{equation}$$

資料來源

---

1. D. P. Kingma and M. Welling, “Auto-Encoding Variational Bayes,” arXiv [stat.ML], 2013. ↩︎

2. Atienza R., 深度學習｜使用 Keras. 碁峰資訊股份有限公司, 2019. ↩︎

3. “相對熵,” Wikipedia.org. [Online]. Available: https://zh.wikipedia.org/zh-tw/相对熵. ↩︎