全面理解：Stable diffusion中的Sampler

簡介

Diffusion model在訓練過程中是將訓練圖集不停加噪，並學習其中的加噪過程，最後可以反向預測圖片的雜訊。所以Diffusion Model的功能基本上是一個雜訊預測器(noise predictor)，透過預測一張圖中的雜訊並扣除來進行降噪，最終獲得一張完整的圖片(或是說，可看得清楚的圖片)。而取樣(sampling)是一種降噪的過程(denoising process)，如圖1之架構圖所示，可基於各種取樣演算法(sampling method)來實現。

圖1 Sampler架構圖

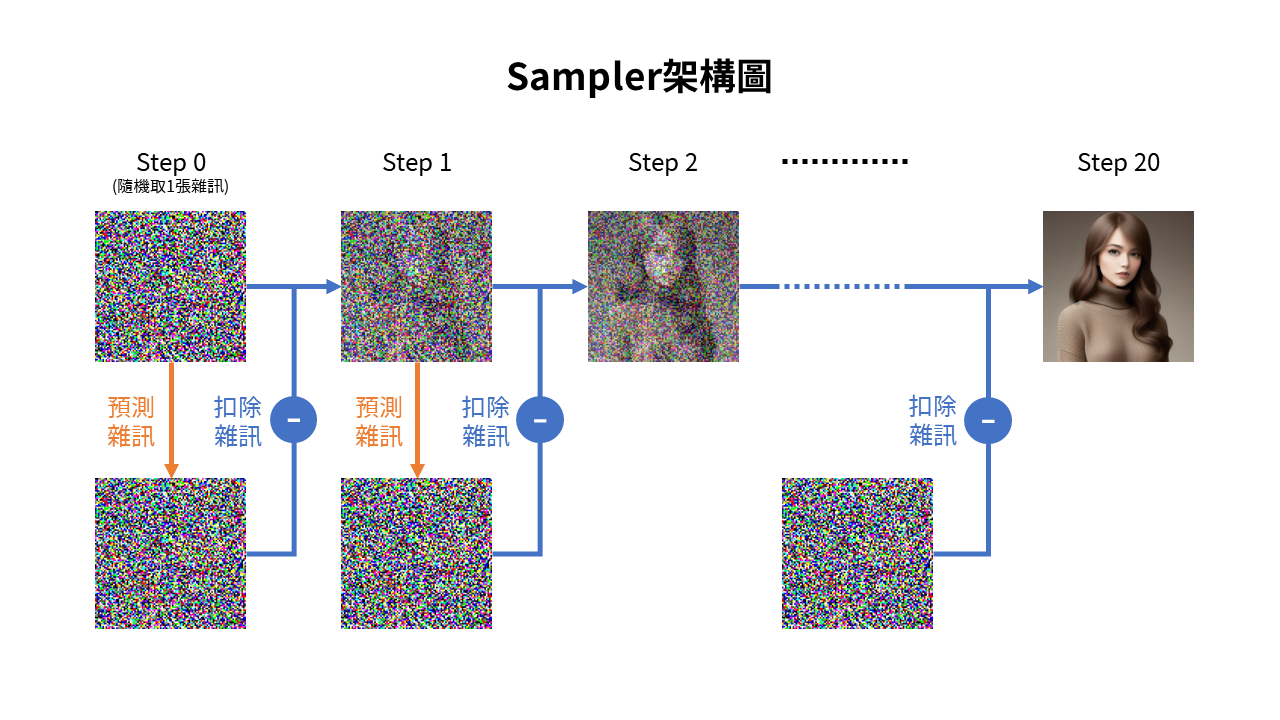
Diffusion model的原始加噪過程是以1000步為基礎，所以理論上降噪也必須執行1000步。而sampler的作用則是在1000步中每n步取樣一次以取得近似解，如step size=20表示將1000步切分取樣20次，因此sampler也稱作scheduler。如此一來可大大降低生成圖片的時間與硬體消耗，並且同時盡量保留原本圖片的樣貌。

各種取樣方法(Sampling method)說明

以下將介紹不同的sampling method之概念：

1. 常微分方程採樣 Ordinary Differential Equations(ODE) Sampler

原論文：Generative Modeling by Estimating Gradients of the Data Distribution
原作者部落格好讀版：https://yang-song.net/blog/2021/score/

宋颺等人提出^[1]，任何SDE可以在不改變邊際分佈的情況下將其轉換為常微分方程(ODE)，因此在求解過程中，我們可將其看作是反向SDE的分布，此ODE稱為probability flow ODE，如下式：

$$dx=[f(x,t)-\frac{1}{2}g^2(t)\nabla_x\log p_t(x)]dt$$

重點摘要

• ODE Sampler是一種近似解。
• Step size會直接影響每次的sampling，也就是說取1步和取10步中的第1步會是不同的結果。
• ODE Sampler是片段線性的採樣。
• ODE比SDE更快，但品質較差。

Stable Diffusion Webui中的ODE方案

• Euler：最簡單的sampler，它使用Euler’s method來解ODE，並且sampling的過程中不會添加任何隨機雜訊。
  *此sampler之實作是在Tero Karras等人於《Elucidating the Design Space of Diffusion-BasedGenerative Models》論文中的Algorithm 2。^[2]

• Heun：改進後的Euler(或稱二階Runge–Kutta法)，相較Euler更加準確但速度較Euler慢約50%，因為它在一次step中先做一次euler並取中間值後，

  $$\overline{y}_{i+1}=y_{i}+hf(t_{i},y_{i})$$

  又再做第二次euler

  $$y_{i+1}=y_{i}+\frac{h}{2}[f(t_{i},y_{i})+f(t_{i+1},\overline{y}_{i+1})]$$

  以取得最終結果。^[3]

  *此sampler之實作來自Tero Karras等人之論文中的Algorithm 1。^[2:1]

• LMS(Linear multistep)：速度和Euler相差無幾，但較準確。因為LMS在sampling時是將以往的所有步數取平均來計算，以提高準確度。^[4]

• PLMS(Pseudo linear multistep)：LMS的變種，是直接在流型上解ODE。^[4:1]

2. 原始採樣 Ancestral samplers

原始採樣在每個sampling step添加隨機雜訊，這使得每次的sampling都會有些微的變化，且每步的sampling只與前次有關，如下式：

$$p(x_1, \dots, x_t)=p(x_1)p(x_2 \mid x_1) \dots p(x_t \mid x_{t - 1})$$

因此，如果想要使每次的生成都有不同的變化(如：飾品、花紋等小細節)，可考慮使用原始採樣。請注意，原始採樣的收斂性(converge)較低，可能會需要較多的step size才能趨近於穩定，且受eta參數影響。

Stable Diffusion Webui的原始採樣方案(有a的即為原始採樣)

• Euler a：Euler的原始採樣版，基於k-diffusion實作。通常可在20~30步內生成良好圖像。^[5]
• DPM++ 2S a
• DPM++ 2S a Karras
• DPM2 a
• DPM2 a Karras

3. DPM(Diffusion Probabilistic Model) Samplers

DPM系列是由北京清華大學的Cheng Lu等人提出的sampling method，分為DPM、DPM++兩代，DPM2則是後人所改良的最新版。

(1) DPM

原論文：DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model...^[6]

• DPM fast：在k-diffusion中實現的固定步長採樣法，可適用於step size<20的情況。
• DPM adaptive：在k-diffusion中實現的自適應步長採樣法。須注意生成速度可能受影響，因為它不保證在指定step size內完成取樣。^[7]

(2) DPM++

原論文：DPM-Solver++: Fast Solver for Guided Sampling of Diffusion...^[8]

DPM++有以下解方：

• 2S a：在k-diffusion中實現二階單步並加入原始採樣法。(原論文之Github提供1/2/3階與單/多步選擇可進行實驗)
• 2M：在k-diffusion中實現二階多步採樣。
• SDE：使用隨機微分方程式(Stochastic Differential Equations)來求解。

Stable Diffusion Webui的DPM++方案

• DPM++原版
  • DPM++ 2S a
  • DPM++ 2M
  • DPM++ SDE
• DPM++ Karras版 (Karras系列詳細介紹請看5. 部分)
  • DPM++ 2S a Karras
  • DPM++ 2M Karras
  • DPM++ SDE Karras

(3) DPM2

由Katherine Crowson在K-diffusion自創並實作的DPM改良版，受sigma與eta參數影響。

Stable Diffusion Webui的DPM2方案

• DPM2原版
  • DPM2
  • DPM2 a
• DPM2 Karras版 (Karras系列詳細介紹請看5. 部分)
  • DPM2 Karras
  • DPM2 a Karras

4. DDIM(Denoising Diffusion Implicit Models) Sampler

原論文：Denoising Diffusion Implicit Models^[9]

• DDIM是由DDPM衍生而來，其採用跳步的方式進行sampling，相較DDPM可節省90%的步數，其生成過程是確定性的。^[10]
• DDIM受eta參數影響。

5. Karras Samplers

原論文：Elucidating the Design Space of Diffusion-Based Generative Models^[2:2]

Karras是由Nvidia研究團隊所研發的sampling method，以第一作者Tero Karras的名子命名。其基於noise schedule來實作sampling，在每次sampling時是將所有的denoise可能性取平均來計算，使需要的sample steps顯著下降，如圖2概念圖所示。

圖2 Karras計算方式概念圖

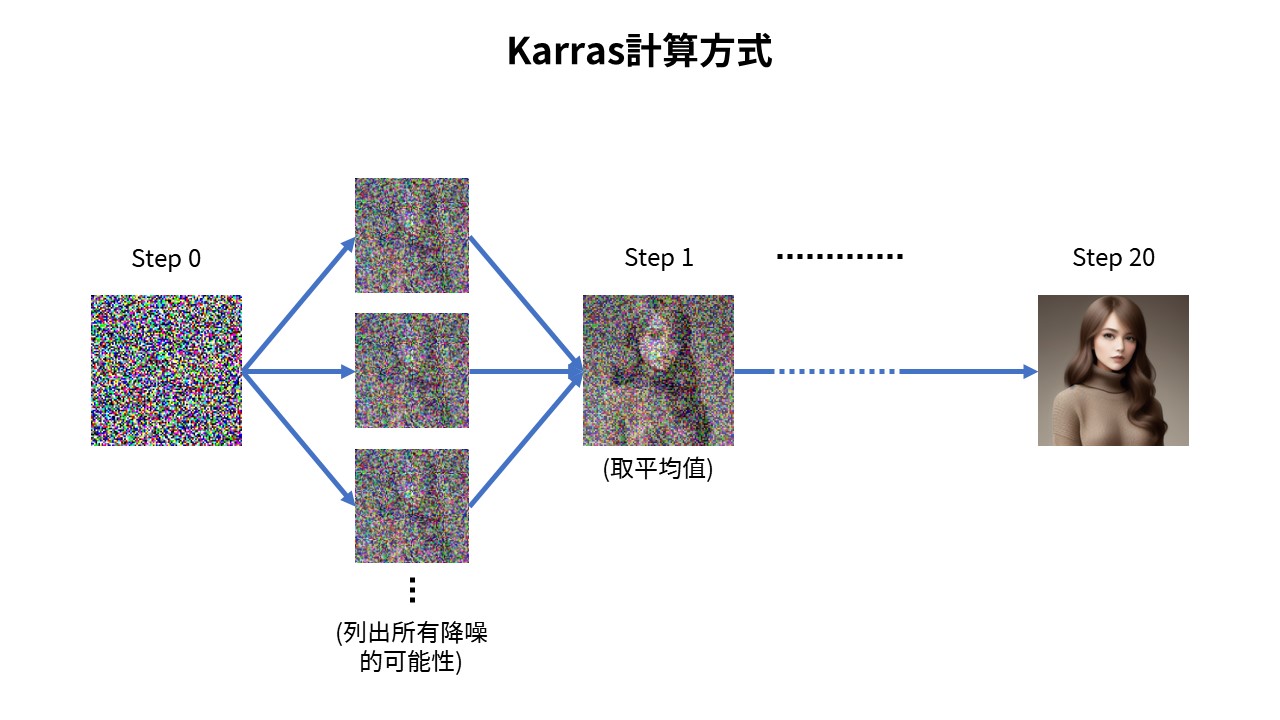
Stable Diffusion Webui的Karras方案

• LMS Karras
• DPM2 Karras
• DPM2 a Karras
• DPM++ 2S a Karras
• DPM++ 2M Karras
• DPM++ SDE Karras

6. UniPC Sampler

原論文：UniPC: A Unified Predictor-Corrector Framework for Fast Sampling...^[11]
原作者部落格好讀版：https://unipc.ivg-research.xyz/

最新的sampler(2023)，由Wenliang Zhao等人所提出。基於ODE Solver中的預測校正的啟發，可在5~10步內產生高品質的圖像。^[7:1]

總結

基本上Sampler(sampling method)的選擇與美觀度較無關聯，只與是否能在最少的step size還原出最接近原圖像有關係。

• 目前以最新的UniPC為首選，因為它可以在最低的step size中產生高品質的圖像。其次可選擇DPM++ 2M與DPM++ 2M Karras。
• 想要每次都有不同變化，可選擇Euler a、DPM++ SDE及DPM++ SDE Karras等。

資料來源

---

1. Y. Song and S. Ermon, “Generative modeling by estimating gradients of the data distribution,” arXiv [cs.LG], 2019. ↩︎

2. T. Karras, M. Aittala, T. Aila, and S. Laine, “Elucidating the design space of diffusion-based generative models,” arXiv [cs.CV], 2022. ↩︎ ↩︎ ↩︎

3. Wikipedia contributors, “Heun’s method,” Wikipedia, The Free Encyclopedia, 07-Jun-2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Heun%27s_method. ↩︎

4. “Samplers,” Stable Diffusion UI v2, 15-Mar-2023. [Online]. Available: https://stable-diffusion-ui.github.io/docs/samplers/. [Accessed: 08-Jul-2023]. ↩︎ ↩︎

5. “Euler Ancestral scheduler,” Huggingface.co. [Online]. Available: https://huggingface.co/docs/diffusers/api/schedulers/euler_ancestral. [Accessed: 08-Jul-2023]. ↩︎

6. C. Lu, Y. Zhou, F. Bao, J. Chen, C. Li, and J. Zhu, “DPM-solver: A fast ODE solver for diffusion probabilistic model sampling in around 10 steps,” arXiv [cs.LG], 2022. ↩︎

7. Andrew, “Stable diffusion samplers: A comprehensive guide,” Stable Diffusion Art, 28-Mar-2023. Available: https://stable-diffusion-art.com/samplers/. ↩︎ ↩︎

8. C. Lu, Y. Zhou, F. Bao, J. Chen, C. Li, and J. Zhu, “DPM-solver++: Fast solver for guided sampling of diffusion probabilistic models,” arXiv [cs.LG], 2022. ↩︎

9. J. Song, C. Meng, and S. Ermon, “Denoising Diffusion Implicit Models,” arXiv [cs.LG], 2020. ↩︎

10. “扩散模型之DDIM,” 知乎专栏. [Online]. Available: https://zhuanlan.zhihu.com/p/565698027. [Accessed: 08-Jul-2023]. ↩︎

11. W. Zhao, L. Bai, Y. Rao, J. Zhou, and J. Lu, “UniPC: A unified predictor-corrector framework for fast sampling of diffusion models,” arXiv [cs.LG], 2023. ↩︎